RECURRENCE INTERVAL

RECURRENCE INTERVAL – In  many  hydraulic-engineering  applications  such  as  those  concerned  with floods, the probability of occurance  of  a  particular  extreme  rainfall,

e.g.  a  24-h maximum  rainfall,  will  be  of  importance.

Such  information  is  obtained  by  the frequency analysis of the point-rainfall data.

The rainfall at a place is a random hydrologic  process and the rainfall data at a place when arranged in chronological order constitute a time series.

One of the commonly used data series is the annual series composed of annual values such as annual rainfall.

If the extreme values of a specified event  occurring in each year is listed, it also constitutes an annual series.

Thus for example, one may list the maximum 24-h rainfall occurring in a year at  a  station  to  prepare  an  annual  series  of  24-h  maximum  rainfall  values.

The probability of occurrence of an event in this series is studied by frequency analysis of this annual data series.

A brief description of the terminology and a simple method of predicting the frequency of an event is described in this section and for details the reader  is referred  to standard  works  on  probability  and  statistics.

The  analysis  of annual series, even though described with rainfall as a reference is equally applicable to any other random hydrological process, e.g. stream flow.

First, it is necessary to correctly understand the terminology used in frequency analysis. The probability of occurrence of an event (e.g. rainfall) whose magnitude is equal to or in excess of a specified magnitude  X is denoted by P.

The recurrence interval (also known as return period) is defined as T=1/P

This represents the average interval between the occurrence of a rainfall of magnitude equal to or greater than X.

Thus if it is stated that the return period of rainfall of 20cm in  24  his  10  years  at  a  certain  station  A,  it  implies  that  on  an  average  rainfall magnitudes equal to or greater than 20 cm in 24 h occur once in 10 years, i.e. in a long period of say 100 years, 10 such events can be expected.

However, it does not mean that every 10 years one such event is likely, i.e. periodicity is not implied.

Then probability of a rainfall of 20 cm in 24 h occurring in any one year at station A is l/T = 1/10 = 0.1.

If the probability of an event occurring is P, the probability of the event not occurring in a given  year is q = ( 1- P).

The binomial distribution  can be used to find  the probability of occurrence of the event r times in n successive years. Thus

where Pr = probability of a random hydrologic event (rainfall) of given magnitude- and  exceedence  probability  P  occurring  r  times  in  n  successive  years.  Thus,  for example,

(a) The probability of an event  of exceedence probability P occurring 2 times inn successive years is

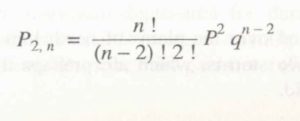
In  using  the  partial  duration  series,  it  is  necessary  to  establish  that  all  events considered are independent.

Hence the partial duration series is adopted mostly  for rainfall analysis where the  conditions of  independency of events are easy to establish its use in flood studies is rather.

The recurrence interval of an event obtained by 100 series (TA) and by the Partial duration ( Tp) are related by

Other links:

HYDROLOGIC CYCLE
PRECIPITATION
RAIN GAUGE
EVAPORATION
INFILTRATION
GROUNDWATER
Water Table
AQUIFER PROPERTIES
DARCY’S LAW
FLOOD FREQUENCY STUDIES
GUMBEL’S METHOD
FLOOD ROUTING